東京大学駒場博物館 特別展「Musica ex
Machina — 機械じかけの音楽」
Hermann
Gottschewski作曲
「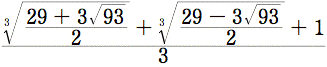 」
」
について
無理数には、複雑なものというイメージが付いてまわります。確かに上にあげた式 — 私の自動ピアノのための作品のタイトルです — は複雑に見えます。この式がどういう数を表しているか計算するのは、コンピュータでなければ不可能に近いでしょう。しかし、これは決して複雑な数ではありません。x3 – x2 = 1
という方程式を満たす価で、およそ1.466になります。
音楽のリズムで使う音の長さ — 「音価」といいます — は比率によって決まります。例えば十六分音符、八分音符、四分音符、二分音符などはすべて 1 : 2 という比率になっています。三拍子、三連符などを使う場合には比率は 1
: 3 です。2 : 3、3 : 4 などの比率も音楽で使われます。例えばピアノ曲で、左手が三連符、右手が普通の八分音符あるいは十六分音符になっている場合がそれに当たります。そういう比率を使うと途中の音が左右の手で合わないので、初心者には難しいリズムになります。でも、比率は無理数ではなく、小さい数字で表すことのできる有理数なので、幾つか合わない音符が続いてもその後でまた合流します。小節の始めの音符はすべて左右の手が一緒に弾きます。だから聴き手も安心して聴けるのです。
音価の比率に無理数を使うと、最初の音では両手が合っていても、その後は二度と合わないことになる、私も以前はそう信じていました。しかし何年か前に、かならずしもそうではないことに気づいたのです。片手のリズムに一つの音価だけでなく、幾つかの音価を混ぜると、無理数を使うことによって初めてリズムが合う場合があるのです。
簡単な例で説明します。音価に「黄金比」を使う工夫をしてみましょう。黄金比とは、 x2 – x = 1 という方程式を満たす価です。書き換えれば、x : 1 = (x + 1) : x になります。約1.618の無理数です。すべての音価をそういう比率にし、ある音価とその次に小さな音価を組み合わせると、その両方を足した時間はちょうどその次に大きな音価になります。つまり、音価がすべて無理数の比率になっているにもかかわらず、上下の音がぴったりと合うのです。次の様にソプラノ、アルト、テノール、バスの四つの声部を、同じリズム、しかも別々のテンポで組み合わせることができますが、その場合テンポの比率は黄金比になるのです。
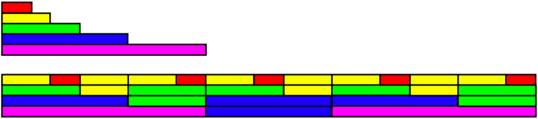
私が自分のこの作品で、もう一段複雑なリズムを使ったのは、その方が一つの声部で三つの音価が混ざり合うため、リズムがさらに面白くなるからです。
そのリズムの元になっている方程式x3 – x2 = 1 を書き換えると x : 1 = (x2 + 1) : x2 になります。つまり、すべての音価をその方程式を満たす価(この作品のタイトルとしてあげた数)の比率にすれば、一つの音価とその二段下の音価を足した合計の時間は一段上の音価になるのです。私の曲のリズム構造は次のようになっています。
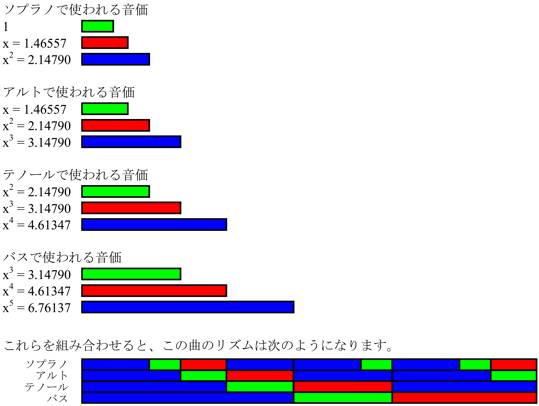
上にあげた黄金比のリズム構造と同様、すべての声部が同じリズムを持ち、そのスピードはそれぞれ1 : 1.466 の比率にあります。
このリズムは、計算するのは難しいかもしれませんが、聴くのは全く難しくありません。「無理数を使ったリズムは聴きやすい」ことを分かってもらうために、私はこの曲を、リズム以外の構造要素ができるだけ「クラッシク風」になるように作りました。クラシック風の和声と対位法を使って、だれでもが歌えるようなメロディーを作ったのです。リズムに集中しなければ全く「普通の音楽」に聴こえると思います。しかし、「普通の音楽」には絶対にありえない、1 : 1.466というテンポ比率を持つ拡大カノンがたくさん使われています。集中して聴く人には分かると思います。この音楽では「普通の音」を使いながら全く新しいことが試みられているのです。
機械でない生身の演奏者にこの様なリズムが再現できるでしょうか。私は、演奏者がこのリズムを聴き慣れれば、可能だと思います。しかし模範演奏をする機械がなかったら、聴き慣れることはできません。その意味で、このリズムは機械があって初めて可能になったものだと言うことができます。


