Sonderausstellung „Musica ex Machina“ im Komaba-Museum
Oktober-Dezember 2007
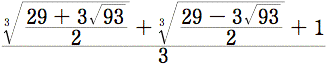
Komposition von Hermann Gottschewski
Diese Komposition war ursprünglich ein Streichquartettsatz
(komponiert 2001), der bisher jedoch wegen seiner irrationalen Rhythmik
nie aufgeführt wurde. Auf der Ausstellung 2007 wurde die Uraufführung
des Werkes in einer Bearbeitung für den Yamaha-Diskflügel realisiert.
Auf der Homepage
von Hermann Gottschewski kann die Fassung von 2007 (mp3
— aiff),
eine Bearbeitung für das Yamaha Stage Piano CP300 von 2009 (mp3
— aiff)
sowie eine weitere Fassung für den Yamaha-Diskflügel angehört
werden, die 2009 an der Musikhochschule Freiburg erarbeitet wurde (mp3
— aiff).
Für die Ermöglichung der letzten Version sowie der Aufnahme beider
Diskflügel-Versionen sei der selbstlosen Unterstützung und
fachkundigen Beratung durch Herrn Professor Sischka und seine Studenten sowie
der Musikhochschule Freiburg für die Bereitstellung des Instrumentes und
der Technik recht herzlich gedankt. In Freiburg entstand auch ein auf Video
dokumentierter Vortrag, dessen Powerpointpräsentation
unter anderem den vollständigen Notentext des Stückes enthält.
Unter „irrationalen Zahlen“ stellen sich die meisten Menschen etwas
Kompliziertes vor. Und ohne Zweifel ist der oben auf dieser Seite stehende
Titel meines Werkes, der in einer mathematischen Formel besteht, nicht auf den
ersten Blick durchschaubar. Um den Wert dieser Formel zu berechnen,
benötigt man mindestens eine gute Rechenmaschine. Dennoch handelt es sich
nicht um eine komplizierte Zahl, sondern um die Lösung der Gleichung x3 – x2 = 1.
Der Wert dieser Lösung ist etwa 1,466.
Die rhythmischen Strukturen komponierter Musik verwenden normalerweise
hauptsächlich die Verhältnisse 1 : 2 und
1 : 3 sowie Potenzierungen und Kombinationen davon. Irrationale
Proportionen kommen nicht vor. (Ob in aufgeführter oder
improvisierter Musik irrationale rhythmische Verhältnisse
vorkommen, lässt sich nicht sagen, da ein irrationales Verhältnis von
einem komplizierten rationalen Verhältnis empirisch nicht unterschieden
werden kann.) Rationale Verhältnisse in der Musik haben den
Vorteil, dass man daraus leicht Strukturen bauen kann, bei denen alles
zueinander passt. Wenn zum Beispiel ein Pianist in der rechten Hand Achtel und
in der linken Hand Achteltriolen spielt, also ein Tempoverhältnis von 2 zu
3 zwischen rechter und linker Hand realisiert, gibt es zwar immer einige
Noten, die nicht gleichzeitig kommen (deshalb ist diese rhythmische Kombination
für Anfänger schwer zu realisieren), aber auf den
Viertelschlägen kommen immer beide Hände gleichzeitig, und somit hat
alles seine Ordnung. Auch der Hörer kann dies leicht nachvollziehen.
Würde man hingegen in zwei Stimmen gleichmäßige Noten in einem
irrationalen Tempoverhältnis spielen, kämen vielleicht am Anfang zwei
Töne gleichzeitig, aber danach nie wieder. Das wäre vollkommen
unmöglich auszuführen, und falls man es doch ausführen
könnte, wäre es für den Hörer sehr verwirrend. (Conlon
Nancarrow hat allerdings solche Werke für mechanisches Klavier
komponiert.)
Ich habe jedoch vor einigen Jahren herausgefunden, dass dies nur gilt, wenn
man gleichmäßige
Noten in beiden Stimmen spielt. Verwendet man hingegen Rhythmen, in denen verschiedene,
in einem irrationalen Verhältnis zueinander stehende Notenwerte vorkommen,
kann man rhythmische Strukturen erzeugen, in denen alles zusammen passt
und auch leicht verständlich klingt. Dieses Werk habe ich komponiert,
um diese Tatsache zu demonstrieren. Ich habe deshalb bewusst darauf
verzichtet, abgesehen vom Rhythmus andere ungewohnte oder neuartige Dinge
einzukomponieren, damit die leichte Verständlichkeit in keiner Weise
beeinträchtigt wird.
Ich möchte, ehe ich die rhythmische Struktur dieses Werkes
erkläre, zunächst mit einem noch einfacheren Beispiel beginnen. Es
gibt ein Verhältnis, das „goldener Schnitt“ genannt wird. Wenn eine
Strecke im Verhältnis des goldenen Schnitts in zwei Teile geteilt wird,
verhält sich der kleinere der beiden Teile zum größeren so wie
der größere Teil zur ganzen Strecke. Es gilt also die Gleichung
1 : x = x : (1 + x). Die Zahl x
drückt das gesuchte Verhältnis aus. Es handelt sich auch um eine
irrationale Zahl, deren Wert etwa 1,618 ist. Die Gleichung lässt sich
umformen zu x2 – x = 1. Sicherlich haben
Sie die Ähnlichkeit zu der oben angegebenen Formel sofort bemerkt. Das
Verhältnis des goldenen Schnittes ist die Lösung einer quadratischen
Gleichung, während das meiner Komposition zugrunde liegende
Verhältnis aus einer kubischen Gleichung hervorgeht.
Wenn man die Notenlängen eines Stückes so festlegt, dass jeder
rhythmische Wert (also jede vorkommende Notenlänge) zum
nächstgrößeren im Verhältnis des goldenen Schnittes steht,
kann in einer Stimme ein rhythmischer Wert mit dem nächstkleineren
Wert kombiniert werden, während eine andere Stimme gleichzeitig den
nächstgrößeren Wert spielt: Die Stimme mit den zwei Noten
teilt dann den rhythmischen Wert der anderen Stimme gerade im Verhältnis
des goldenen Schnittes. Wie unten gezeigt, könnte man in einer
solchen Komposition einen rhythmischen Kanon ausführen, in dem
die Stimmen im Tempoverhältnis des goldenen Schnittes zueinander
stehen. Das heißt, die Stimmen würden exakt den selben Rhythmus in
verschiedenem Tempo ausführen. Trotz des irrationalen
Tempoverhältnisses würden alle Stimmen synchron zueinander
fortschreiten. Im Prinzip könnte man beliebig viele Stimmen so
kombinieren. Für einen vierstimmigen Satz bräuchte man fünf
verschiedene Notenwerte, die zueinander im Verhältnis des
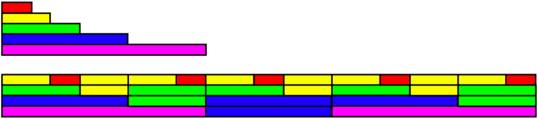
goldenen Schnittes stehen. In der Graphik unten sind zunächst die
fünf Notenwerte in ihrem Längenverhältnis durch
verschiedenfarbige Balken, dann die Kombination der Notenwerte im
vierstimmigen Satz dargestellt. Jede einzelne Stimme benutzt nur zwei
verschiedene Notenwerte.
In meiner Komposition habe ich etwas sehr ähnliches gemacht, nur eine
Spur komplexer. Ich habe Notenwerte verwendet, die genau in demjenigen
Verhältnis zueinander stehen, bei dem die Kombination eines Wertes
mit dem übernächst kleineren den
nächstgrößeren Wert ergibt. Dadurch wird die rhythmische
Struktur etwas komplizierter: es sind drei verschiedene Notenwerte
in einer Stimme notwendig, um zu einer synchronen Kombination zu kommen. Dementsprechend
ist es musikalisch interessanter. Außerdem wird jetzt ein rhythmischer
Kanon im Tempoverhältnis 1 : 1,466 möglich,
d.h. die Stimmen unterscheiden sich in ihrem Tempo weniger als im Falle
des goldenen Schnittes. Dadurch kann ein vierstimmiger rhythmischer Kanon noch
gut ausgeführt werden, ohne dass es in den Außenstimmen zu
extremen Tempi kommt.
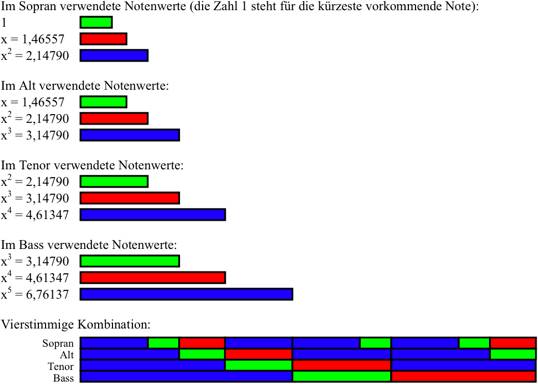
Unten ist genau die rhythmische Struktur dargestellt, die ich in meinem
Stück verwendet habe. Wie in dem Beispiel mit dem goldenen Schnitt beruht
sie auf einem strengen rhythmischen Kanon zwischen allen Stimmen. Im
Mittelteil gibt es auch einen durch alle vier Stimmen gehenden melodischen
Kanon, was allerdings schwierig zu hören ist. Leichter zu hören ist,
wie im Anfangs- und Schlussteil ein neuntöniges Motiv nacheinander in
Sopran, Alt, Tenor und Bass gespielt wird, wobei das Tempo jedes Mal im
Verhältnis 1 : 1,466 langsamer wird. Um den rhythmischen
Kanon optisch deutlicher zu machen, habe ich in der folgenden Graphik
die Farben nicht für konstante rhythmische Werte, sondern relativ zum
Tempo der jeweiligen Stimme eingesetzt.
Vielleicht
gehören Sie zu den Menschen, denen alles, was mit Zahlen und Formeln zu
tun hat, kompliziert vorkommt. Aber hören Sie bitte hin: Es klingt
gar nicht kompliziert. Ich glaube, dass Musiker schnell in der Lage wären,
diese neue Rhythmik zu erlernen. Nach einer kurzen Phase der
Gewöhnung erschließen sich aber neue Dimensionen der Rhythmus- und
Tempoerfahrung.


